ホイル＝リットルトン降着
ホイル＝リットルトン降着 (Hoyle-Lyttleton accretion)は，
HoyleとLyttletonが1939年に提案したもので，
重力天体への質量降着の基本的なメカニズムである．
十分調べ尽くされたように思える，このきわめて古典的な問題が，
“中心天体の輻射場”という光を当てることにより，
新たな現代的問題として甦った．
Reference: 日本語版
\begin{center}
{\bf Abstract}
\end{center}
We investigate Hoyle--Lyttleton accretion
for the case where the central source is
a luminous accretion disk.
%
In classical Hoyle-Lyttleton accretion onto a ``spherical'' source,
accretion takes place in an axially symmetric manner
around a so-called accretion axis.
In the spherical case
the accretion rate $\dot{M}$ is given as
$\dot{M}_{\rm HL} (1-\Gamma)^2$,
where
$\dot{M}_{\rm HL}$ is the accretion rate of
the classical Hoyle--Lyttleton accretion onto a non-luminous object
and $\Gamma$ the luminosity of the central object
normalized by the Eddington luminosity.
%
If the central object is a compact star
with a luminous accretion disk,
the radiation field becomes ``non-spherical''.
%although the gravitional field remains spherical.
In such a case
the axial symmetry around the accretion axis breaks down;
the accretion radius $R_{\rm acc}$ generally depends on
an inclination angle $i$ between the accretion axis
and the symmetry axis of the disk
and the azimuthal angle $\varphi$ around the accretion axis.
%That is, the cross section of accretion changes its shape.
Hence,
the accretion rate $\dot{M}$,
which is obtained by integrating $R_{\rm acc}$ around $\varphi$,
depends on $i$.
% as well as $M$, $\Gamma$, and $v_\infty$.
%
In the case of a pole-on accretion ($i=0$),
although the axisymmetry around $\varphi$ is retained,
the accretion radius becomes smaller than
that of the spherical case.
The accretion rate is therefore smaller than
that of the spherical case.
We found that the accretion rate is approximately expressed as
$\dot{M} \sim \dot{M}_{\rm HL} (1-\Gamma)(1-2\Gamma)$.
%
In the case of an edge-on accretion ($i=90^{\circ}$),
the accretion radius depends strongly on $\varphi$
and is somewhat larger than that of the spherical case.
Depending on the central luminosity $\Gamma$,
the shape of the accretion cross-section varies from
a circle ($\Gamma=0$), an ellipse,
a hollow ellipse ($\Gamma \sim 0.5$), and
a twin lobe ($\Gamma \gsim 0.65$).
The accretion rate is larger than that of the spherical case
and approximately expressed as
$\dot{M} \sim \dot{M}_{\rm HL} (1-\Gamma)$ for $\Gamma \leq 0.65$
and
$\dot{M} \sim \dot{M}_{\rm HL} (2-\Gamma)^2/5$ for $\Gamma \geq 0.65$.
%
Once the accretion disk forms and
the anisotropic radiation fields are produced
around the central object,
the anisotropic nature around the azimuthal angle
will maintain the accretion plane.
%
%Thus, the anisotropic radiation fields of accretion disks
%drastically change the accretion nature.
%
Hoyle--Lyttleton type accretion onto the accretion disk
may take place in various astrophysical situations,
including the Galactic Center X-ray source 1E~1740.7$-$2942.
■ホイル＝リットルトン降着とは？
Accretion onto the gravitating body
is one of most important phenomena in recent astrophysics,
since it produces and radiates a remarkable energy
via the release of the gravitational energy (e.g., Kato et al. 1998).
If the central object is a compact star,
a significant fraction of the rest mass energy of
the accreting gas is liberated.
Furthermore, an energetic mass outflow from the accretion system
often takes place.
Thus, the central engine of the accretion system
exerts a strong influence on the environments
through intense radiation and mass outflow.
If there is an isolated object in interstellar space,
the gravitational field of the object
attracts the gas particles.
If there exists a relative velocity
between the object and the gas,
the gas particles move in hyperbolic orbits,
which intersect downstream of the point mass
on the axis of symmetry (the accretion axis).
The intersecting particles are allowed to collide
and coalesce on the accretion axis.
Particles colliding sufficiently close to the point mass lose
enough of their kinetic energy to be trapped by the central object.
This is a classical picture of
Hoyle--Lyttleton accretion
(Hoyle, Lyttleton 1939; Bondi, Hoyle 1944).
Let us suppose
a graviating body with mass $M$ and luminosity $L$,
which is placed in a gas flow
with velocity $v_{\infty}$ and density $\rho_{\infty}$
at infinity.
If the velocity $v_{\infty}$ is much larger
than the sound speed of the gas at infinity,
the pressure effect can be neglected,
except for at the very center.
Then, the Hoyle--Lyttleton accretion radius $R_{\rm HL}$,
where the effect of radiation pressure is ignored, is
\begin{eqnarray}
R_{\rm HL} &=& \frac{2GM}{v_{\infty}^2}
\nonumber \\
&=& 2.65 \times 10^{15}
\frac{M}{10M_{\odot}}
\left( \frac{v_\infty}{10{\rm ~km~s}^{-1}} \right)^{-2}
{\rm ~cm}.
\end{eqnarray}
In addition, the relevant timescale of
the classical Hoyle--Lyttleton accretion is
\begin{eqnarray}
t_{\rm HL} &=& \frac{R_{\rm HL}}{v_\infty}
\nonumber \\
&=& 84.0
\frac{M}{10M_{\odot}}
\left( \frac{v_\infty}{10{\rm ~km~s}^{-1}} \right)^{-3}
{\rm ~yr}.
\label{tHL}
\end{eqnarray}
Inside the accretion radius
the potential energy exceeds the kinetic energy
and the gas is trapped by the gravitating object.
Thus, the mass accretion rate ${\dot M}_{\rm HL}$
onto the gravitating object is
\begin{eqnarray}
{\dot M}_{\rm HL} &=& \pi R_{\rm HL}^2 \rho_{\infty} v_{\infty}
= \frac{4\pi\rho_{\infty}G^2 M^2}{v_{\infty}^3}
\nonumber \\
&=& 3.70 \times 10^{18}
\left( \frac{M}{10M_{\odot}} \right)^2
\frac{n_\infty}{10^5 {\rm ~cm}^{-3}}
\left( \frac{v_\infty}{10{\rm ~km~s}^{-1}} \right)^{-3}
{\rm ~g~s}^{-1},
\end{eqnarray}
where $n_\infty$ is the number density at infinity.
In addition, the growth time of the central object is
\begin{eqnarray}
t_{\rm growth} &=& \frac{M}{\dot{M}_{\rm HL}}
\nonumber \\
&=& 1.70 \times 10^8
\left( \frac{M}{10M_{\odot}} \right)^{-1}
\left( \frac{n_\infty}{10^5 {\rm ~cm}^{-3}} \right)^{-1}
\left( \frac{v_\infty}{10{\rm ~km~s}^{-1}} \right)^{3}
{\rm ~yr}.
\label{tgrowth}
\end{eqnarray}
If we know the accretion rate,
we can estimate the (accretion) luminosity of the radiation
emitted from the compact object.
Therefore, knowledge about the accretion radius is important
to compare theories with observations.
%
■中心天体が光っているとき：輻射圧の影響
The effect of gas pressure on Hoyle--Lyttleton accretion
has been investigated by many researchers
(Bondi 1952; Hunt 1971; Shima et al. 1985; Fryxell et al. 1987;
Ho et al. 1989; Koide et al. 1991).
The effect of radiation pressure, however,
has not been taken into account well (e.g., Taam et al. 1991).
Due to radiation pressure,
the accretion radius and the accretion rate
are significantly reduced from the Hoyle--Lyttleton estimate.
That is,
the accretion radius modified by the radiation pressure becomes
\begin{equation}
R_{\rm HL}^{\rm rad}=\frac{2GM(1-\Gamma)}{v_{\infty}^2}
=R_{\rm HL}(1-\Gamma),
\label{eqn:bondi}
\end{equation}
when the gas is fully ionized and transparent.
Here, $\Gamma$ is the normalized luminosity,
which is defined by the ratio of the luminosity $L$
of the gravitating object to the Eddington luminosity
$L_{\rm E}$ ($=4 \pi cGMm_{\rm p}/\sigma_{\rm T}$):
\begin{equation}
\Gamma = \frac{L}{L_{\rm E}},
\end{equation}
where $m_{\rm p}$ is the proton mass
and $\sigma_{\rm T}$ the Thomson scattering cross-section.
In this case with radiation pressure,
$\dot{M}=\dot{M}_{\rm HL}(1-\Gamma)^2$.
■輻射抵抗の効果
Recently,
the effect of radiation drag (Compton drag)
in Hoyle--Lyttleton accretion around a luminous source
was also considered by Nio et al. (1998).
%
In the ionized gas the radiation-drag force becomes important
if the velocity of the gas is comparable to the light speed
and the luminosity of the central object is
comparable to the Eddington luminosity.
Radiation drag is also important
if the specific cross-section --- ``opacity'' ---
of particles is sufficiently large like, e.g., dust.
%
Nio et al. (1998) found that
the accretion radius decreases due to radiation pressure,
while it increases due to radiation drag.
In addition, the accretion radius considering radiation drag
becomes larger as the incident velocity becomes fast.
In the limit of small $v_\infty$,
the above equation (\ref{eqn:bondi}) is modified as
$R_{\rm HL}^{\rm rad}/R_{\rm HL} = 1 - \Gamma (1-2v_\infty/c)$.
■降着円盤へのホイル＝リットルトン降着
In all of these studies
the central sources have been supposed to be ``spherical'';
both of the gravitational and radiation fields
have a spherical symmetry.
In actual accretion systems
like the Galactic Center X-ray source 1E~1740.7$-$2942, however,
as a consequence of mass accretion,
an accretion disk often forms
around the central gravitating body.
Hence, in such a case
the radiation field is not spherical but ``anisotropic''.
That is, the radiative flux $F$ at a distance $R$ from the center
depends on a polar angle $\theta$ as
\begin{equation}
F= \frac{L}{2\pi R^2} \cos \theta,
\label{diskF}
\end{equation}
where $L$ is the total luminosity of the disk.
The accretion radius and therefore the mass accretion rate
will be changed due to the violation of the spherical symmetry.
Indeed, the anisotropic radiation fields
drastically change the accretion nature.
The purpose of this paper is thus to examine
the Hoyle--Lyttleton accretion onto the accretion disk.
\begin{flushleft}
{\bf 2. Situations and Basic Equations}
\end{flushleft}
\begin{flushleft}
{\it 2.1. Radiation Fields}
\end{flushleft}
Let us consider
a point mass with mass $M$ and
a surrounding accretion disk with luminosity $L$ (figure 1).
The system is assumed to be immersed in uniform gas flow
with velocity $v_\infty$ and density $\rho_\infty$.
We also assume that the gas is fully ionized and transparent
to radiation from the object.
The central accretion disk is generally
inclined to the gas flow
(the inclination angle between
the accretion axis and the symmetry axis of the disk
is $i$).
%
We adopt cylindrical coordinates $(r, \varphi, z)$,
where the $z$-axis ({\it accretion axis}) is in
the direction of the upstream gas particles (see figure 1).
Moreover, the coordinates of a particle coming from infinity
are $(x, y, z)$ in Cartesian coordinates and
$(R, \theta, \varphi)$ in spherical coordinates
($R=\sqrt{r^2+z^2})$.
In this system
we first derive the radiative flux vector
at a point P, where a particle is located.
\begin{center}
------------ \\
figure 1 \\
------------ \\
\end{center}
In Cartesian coordinates,
the unit vector $\bmi$
in the direction of the symmetry axis of the disk,
and the unit vector $\bms$
in the direction of a particle are respectively
\begin{eqnarray}
\bmi &=& \left( \sin i, 0, \cos i \right),
\\
\bms &=& \left( \frac{r}{R}\cos\varphi,
\frac{r}{R}\sin\varphi, \frac{z}{R} \right).
\end{eqnarray}
Hence, the angle $\psi$ between
the symmetry axis $\bmi$ and the particle direction $\bms$ is
given by
\begin{equation}
\cos \psi = {\bmi} \cdot {\bms}
= \frac{1}{R}
\left( r\cos \varphi \sin i + z \cos i \right).
\end{equation}
The radiative flux $F_R$ in the $R$-direction
at a point is expressed as
\begin{equation}
F_R = \frac{L \cos \psi}{2\pi R^2}.
\label{FR}
\end{equation}
Consequently, the radial component $F_r$ and
the vertical component $F_z$ in cylindrical coordinates are,
respectively,
{
\setcounter{enumi}{\value{equation}}
\addtocounter{enumi}{1}
\setcounter{equation}{0}
\renewcommand{\theequation}{\theenumi\alph{equation}}
\begin{eqnarray}
F_r &=& F_R \frac{r}{R},
\\
F_z &=& F_R \frac{z}{R}.
\end{eqnarray}
\setcounter{equation}{\value{enumi}}
}
It should be noted that
if the distance from the center is of the order of the disk size,
the radiation fields of the disk
becomes much more complicated (cf. Tajima, Fukue 1998)
and the above formula becomes inadequate.
\begin{flushleft}
{\it 2.2. Basic Equations}
\end{flushleft}
The motion of the gas particle in radiation fields
is described by
\begin{equation}
\frac{d\bmv}{dt}
=-\bmnabla \phi + \frac{\sigma_{\rm T}}{mc}
(\bmF-E \bmv -{\bf P} \otimes \bmv)
\label{vector}
\end{equation}
upto the first order of $v/c$,
where $\bmv$ is the particle velocity,
$\phi$ the gravitational potential,
$m$ the particle mass (proton mass for the normal plasma),
$E$ the radiation energy density,
$\bmF$ the radiative flux vector,
and {\bf P} the radiation stress tensor
(Hsieh, Spiegel 1976; Fukue et al. 1985;
see also Kato et al. 1998).
In Nio et al. (1998),
in order to examine the effect of radiation drag,
they considered the radiation energy and
the radiation stress tensor as well as the radiative flux.
In the present study
we only consider the radiative flux
to avoid the complication
and to focus our attention on the anisotropic feature
of the radiation field.
Thus, the equation of motion
in cylindlical coordinates $(r, \varphi, z)$
is expressed as
{
\setcounter{enumi}{\value{equation}}
\addtocounter{enumi}{1}
\setcounter{equation}{0}
\renewcommand{\theequation}{\theenumi\alph{equation}}
\begin{eqnarray}
\frac{\displaystyle dv_r}{\displaystyle dt}
&=& -\frac{\displaystyle GMr}{\displaystyle R^3}
+\frac{\displaystyle \sigma_{\rm T}}{\displaystyle mc}
F_R \frac{\displaystyle r}{\displaystyle R},
\\
\frac{\displaystyle dv_z}{\displaystyle dt}
&=& -\frac{\displaystyle GMz}{\displaystyle R^3}
+\frac{\displaystyle \sigma_{\rm T}}{\displaystyle mc}
F_R \frac{\displaystyle z}{\displaystyle R}.
\label{eqn:basiceq0}
\end{eqnarray}
\setcounter{equation}{\value{enumi}}}
Using equation (\ref{FR}),
the above equation of motion becomes
{
\setcounter{enumi}{\value{equation}}
\addtocounter{enumi}{1}
\setcounter{equation}{0}
\renewcommand{\theequation}{\theenumi\alph{equation}}
\begin{eqnarray}
\frac{\displaystyle dv_r}{\displaystyle dt}
&=&-\frac{\displaystyle GMr}
{\displaystyle R^3}(1-\Gamma_{\rm eff}),
\\
\frac{\displaystyle dv_z}{\displaystyle dt}
&=&-\frac{\displaystyle GMz}
{\displaystyle R^3}(1-\Gamma_{\rm eff}),
\end{eqnarray}
\setcounter{equation}{\value{enumi}}}
where $\Gamma_{\rm eff}$ is the {\it effective} normalized luminosity
defined by
\begin{eqnarray}
\Gamma_{\rm eff} &\equiv& 2 \Gamma \cos\psi
\nonumber \\
&=& 2\frac{L}{L_{\rm E}}
\frac{ r\cos \varphi \sin i + z \cos i }
{R}.
\end{eqnarray}
%where $L_{\rm E}$ ($=4 \pi cGMm_{\rm p}/\sigma_{\rm T}$)
%is the Eddington luminosity of the central object.
Measuring the length and velocity in units of
$R_{\rm HL}$ and $v_\infty$, respectively,
and using the relevant timescale $t_{\rm HL}$,
the equation of motion is finally rewritten in the dimensionless form:
{
\setcounter{enumi}{\value{equation}}
\addtocounter{enumi}{1}
\setcounter{equation}{0}
\renewcommand{\theequation}{\theenumi\alph{equation}}
\begin{eqnarray}
\frac{\displaystyle d\hat{v}_r}{\displaystyle d\hat{t}}
&=&-\frac{\displaystyle \hat{r}}
{\displaystyle 2\hat{R}^3}(1-\Gamma_{\rm eff}),
\\
\frac{\displaystyle d\hat{v}_z}{\displaystyle d\hat{t}}
&=&-\frac{\displaystyle \hat{z}}
{\displaystyle 2\hat{R}^3}(1-\Gamma_{\rm eff}).
\label{eqn:basiceq}
\end{eqnarray}
\setcounter{equation}{\value{enumi}}}
For various combinations of initial positions $(r, \varphi)$
of particles at sufficiently large $z$,
we numerically integrate equation (17)
using the forth-order Runge--Kutta--Gill method
and calculate trajectories of particles.
%
We estimate the accretion radius by the same procedure
as that of Hoyle and Lyttleton (1939).
That is, according to parameters,
particles intersect the accretion axis
at the downstream of the axis.
If the $z$-velocity is less than the escape velocity
at that point ($z=z_0$),
defined by
$\hat{v}_{\rm esc}=\sqrt{(1-\Gamma_{\rm eff})/\hat{z}}|_{r=0, z=z0}$,
these particles are judged to be
captured and accreted on the gravitating body.
The parameters of the present problem are
the normalized luminosity $\Gamma$,
the incident velocity $v_\infty$
(although $v_\infty$ is renormalized in the unit), and
the disk inclination angle $i$.
%
In the present study
we only examine two extreme cases;
a pole-on accretion ($i=0$) and an edge-on one ($i=90^{\circ}$).
Other general cases with arbitrary $i$ lie
between these two cases.
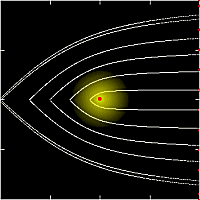
Figure 2 shows the accretion radius $R_{\rm acc}$
normalized by the Hoyle--Lyttleton accretion radius $R_{\rm HL}$
($=2GM/v_{\infty}^2$)
as a function of the normalized luminosity $\Gamma$ ($=L/L_{\rm E}$).
%in the case of $v_{\infty}=0.1c$.
\begin{center}
------------ \\
figure 2 \\
------------ \\
\end{center}
The dotted straight line is for the case of a spherical source,
that is proportional to $(1-\Gamma)$,
as shown in equation (\ref{eqn:bondi}).
The dashed curve is the pole-on accretion case ($i=0$),
where the accretion radius is independent of $\varphi$.
As already stated in equation (\ref{diskF}),
the disk radiation field is not spherical but
orients towards the polar direction.
Hence, in the pole-on accretion of $i=0$,
the central source (disk) is effectively luminous,
compared with the spherical case.
As a result,
the accretion radius is remarkably smaller than
that of the spherical case, as seen in figure 2.
The solid curves are the edge-on accretion case ($i=90^{\circ}$),
where the accretion radius is strongly depends on $\varphi$.
In this case
the situation is much more complicated,
because the radiation strength varies along the particle path
and depends on $\varphi$.
Roughly speaking, however,
in the edge-on accretion of $i=90^{\circ}$,
the disk is effectively less luminous,
and the accretion radius is larger than
that of the spherical case.
In figure 3
the shapes of cross section in the case of $i=90^{\circ}$
are shown for various $\Gamma$.
Since incoming particles in the disk plane ($\varphi=90^{\circ}$)
receive no radiative flux,
the accretion radius in the disk plane
is just the classical Hoyle--Lyttleton one $R_{\rm HL}$.
On the other hand,
particles travelling over the disk are so influenced
by the disk radiation field that
the accretion radius becomes smaller than $R_{\rm HL}$.
Moreover, particles passing through just above the pole
($\varphi=0$)
cannot accrete for $\Gamma \gsim 0.65$.
As a result,
depending on the normalized luminosity $\Gamma$,
the shape of the accretion cross-section varies
from a circle ($\Gamma=0$),
an ellipse compressed perpendicular to the disk plane,
a hollow ellipse ($\Gamma \sim 0.5$),
and a twin lobe in the disk plane ($\Gamma \gsim 0.65$).
\begin{center}
------------ \\
figure 3 \\
------------ \\
\end{center}
Since in the present situation
the accretion radius $R_{\rm acc}$ generally depends on $\varphi$,
the cross sectional area of accretion is more convenient
to discuss the accretion nature.
In addition, the cross sectional area $A_{\rm acc}$ of accretion
is directly related to the accretion rate by
$\dot{M}= A_{\rm acc} \rho_\infty v_\infty$.
In figure 4 we show
the cross sectional area $A_{\rm acc}$,
normalized by that of
the Hoyle--Lyttleton accretion, $\pi R_{\rm HL}^2$,
as a function of the normalized luminosity $\Gamma$
(this also expresses $\dot{M}/\dot{M}_{\rm HL}$).
%in the case of $v_{\infty}=0.1c$.
As expected from the accretion radius calculated above,
the accretion rate in the pole-on case is smaller than
that of the spherical case.
The accretion rate in the edge-on case, on the other hand,
is larger than that of the spherical case.
It should be noted that in the edge-on case
accretion is possible even if $\Gamma$ is unity!
\begin{center}
------------ \\
figure 4 \\
------------ \\
\end{center}
Finally, from these numerical results,
the cross sectional area $A_{\rm acc}$
is approximately expressed as
\begin{equation}
A_{\rm acc} = \pi R_{\rm HL}^2 f(\Gamma, i),
\end{equation}
where
\begin{equation}
f\left(\Gamma, i\right) = \left\{
\begin{array}{ll}
(1-\Gamma)^2 & ~~~{\rm for~a~spherical~case} \\
(1-\Gamma)(1-2\Gamma) & ~~~{\rm for~}i=0 \\
(1-\Gamma) & ~~~{\rm for~}i=90^{\circ}, \Gamma \leq 0.65 \\
(2-\Gamma)^2/5 & ~~~{\rm for~}i=90^{\circ}, \Gamma \geq 0.65.
\end{array}
\right.
\label{f}
\end{equation}
\begin{flushleft}
{\bf 5. Discussion}
\end{flushleft}
In this section
we shall briefly discuss
the astrophysical implications and applications of
the present Hoyle--Lyttleton accretion onto accretion disks.
\begin{flushleft}
{\it 5.1. Maintenance of the Disk Plane}
\end{flushleft}
As shown in the previous sections,
the anisotropic radiation fields of accretion disks
may drastically change the accretion nature of
the classical Hoyle--Lyttleton accretion.
%i)
First, let us suppose the edge-on accretion ($i=90^{\circ}$).
Because of the anisotropy of radiation fields,
the accretion radius over the disk poleward becomes small,
compared with that in the disk plane (see figure 3).
In other words, accretion takes place mainly
in the disk plane.
This nature,
that {\it the prefered accretion plane coincides with the disk plane},
operates so as to maintain the accretion disk further.
Naively speaking, of course,
net angular momentum of the accreting gas in the disk plane is zero.
Hence, the spin direction of the disk
may interchange through flip-flop mechanisms
with timescale of $t_{\rm HL}$.
However, the disk always forms continually
with a fixed axis of symmetry.
%
These properties are essentially same in general cases
with arbitrary inclination angle,
except for the pole-on accretion.
%ii)
Then, let us suppose the longterm behavior of the accretion.
As is seen from figure 4,
the accretion rate of the edge-on case is larger than other cases;
the edge-on accretion is the most effective.
Hence, if the disk initially inclined to the gas flow
with arbitrary inclination angle,
the inclination angle gradually increases, as accretion proceeds.
Ultimately,
the disk configuration will settle down
in such a state that the disk axis becomes
perpendicular to the accretion axis;
the edge-on accretion would be finally established.
%iii)
Finally, let us suppose
the origin and maintenance of accretion disks,
which form around the gravitating object
under the Hoyle--Lyttleton accretion process.
At the first stage,
where only the gravitating body exists in the interstellar space,
there is no preferable direction of accretion.
That is,
the classical Hoyle--Lyttleton accretion takes place
symmetrically around the accretion axis.
After the Hoyle--Lyttleton accretion proceeds,
some possible irregularities in the gas density or velocity
breaks down the symmetry of accretion around the accretion axis.
Due to this spontaneous breaking of symmetry,
an accretion disk forms and a prefered direction is fixed.
Once the disk forms,
the prefered direction and the disk plane
may be maintained, as discussed above.
If astrophysical jets emanate from the disk,
the direction of jets is also maintained.
\begin{flushleft}
{\it 5.2. Application to 1E~1740.7$-$2942}
\end{flushleft}
We here apply the present model
to the Galactic Center X-ray source 1E~1740.7$-$2942.
Electron-positron pair annihilation lines
from the Galactic Center region
have been detected since 1970's
(e.g., Johnson et al. 1972; see Morris 1989 for a review).
The intensity of annihilation lines is about
$10^{-3}$photons s${}^{-1}$ cm${}^{-2}$,
and this yields the positron annihilation rate of $10^{43}$ s${}^{-1}$
with the distance to the Galactic Center
(Johnson, Haymes 1973; Leventhal et al. 1978).
The lack of significant redshift and the narrowness of the line width
suggest that the pair annihilation takes place
in relatively cold gas.
Recent observations by the GRANAT satellite identified
the pair annihilation source to the hard X-ray source 1E~1740.7$-$2942
near the Galactic Center
(Sunyaev et al. 1991; Bouchet et al. 1991).
Then, this X-ray source 1E~1740.7$-$2942 was found to be embedded
in the molecular cloud which belongs to the inner molecular layer
of the Galactic Center region
(Mirabel et al. 1991; see also Ramaty et al. 1992).
%%%%%%%%%%%%
This cloud has a size of $\sim$ 3pc and a mean density of
$\sim 5\times 10^4 {\rm cm}^{-3}$,
therefore, has a mass of $\sim 5 \times 10^4 M_{\odot}$.
Finally, by the observation with the Very Large Array
(Mirabel et al. 1992),
a double-sided radio jet from this X-ray source 1E~1740.7$-$2942 has found.
The projected length of this radio jet is $\sim$ 1pc.
Various observational facts suggest the following picture
for the X-ray source 1E~1740.7$-$2942 and the radio jet
(Mirabel et al. 1991, 1992).
The X-ray source 1E~1740.7$-$2942 may be
a stellar mass black hole without companion
--- an {\it isolated black hole}
(the X-ray spectrum of 1E~1740.7$-$2942 resembles that of Cyg~X-1).
From a molecular cloud,
the interstellar gas accretes onto this black hole
via the Hoyle--Lyttleton process,
an accretion disk forms around the black hole,
and electron-positron pairs are created
in the vicinity of the black hole.
The electron-positron pair plasma are ejected
perpendicular to the disk plane (cf. Tajima, Fukue 1998), and then injected
into the molecular cloud in the form of a double-sided jet
(the radio emission from jets is supposed to be synchrotron radiation
from electrons and positrons).
Electron-positron pairs travel at high velocities for a few years
and then they are slow down and annihilated
in the high-density cold molecular cloud
(the annihilation lines are narrow).
Now, using the observational facts described above and
physical quantities deduced from observations (in the appendix),
we shall estimate the plausible accretion rate
and the intrinsic luminosity of 1E~1740.7$-$2942.
We first evaluate the relative velocity $v_\infty$ at infinity
through the geometrical reason and activity duration.
As already discussed,
in Hoyle--Lyttleton accretion onto the accretion disk,
the symmetry axis of the disk generally tends to lie
in the plane perpendicular to the flow direction.
If this is true for the case of 1E~1740.7$-$2942,
the black hole moves transversely perpendicular to the line-of-sight,
and the transverse velocity is of the order of $v_\infty$.
VLA observations show that
the jets in 1E~1740.7$-$2942 are rather straight
and no prominent bending is seen.
This geometrical properties mean that
the ratio of the transverse velocity to the jet velocity
is less than $\sim 10^4$.
Since the jet velocity is estimated as $0.3c$ in the appendix,
the transverse velocity and therefore $v_\infty$ is about
$v_\infty \lsim 10 {\rm ~km~s}^{-1}$.
%
On the other hand, from
the projection length of jets ($\sim$ 1~pc)
and the jet velocity ($0.3c$),
the central activity producing jets lasts
at least 10~yrs.
Due to the flip-flop mechanism,
the direction of the disk rotation changes intermittently.
Indeed, the electron-positron annihilation features
disappear in a timescale of a few years.
These dynamical variations occur in the timescale of $t_{\rm HL}$
given in equation (\ref{tHL}).
Hence, the activity timescale again means that
$v_\infty \sim 10 {\rm ~km~s}^{-1}$
as long as $M \sim 10M_{\odot}$.
Thus, for 1E~1740.7$-$2942, since
the mass $M$ is reasonably assumed to be $10M_{\odot}$,
a mean density of the ambient cloud is observed to be
$\sim 5\times 10^4 {\rm cm}^{-3}$, and
the velocity $v_\infty$ is derived to be $\lsim 10 {\rm ~km~s}^{-1}$,
we can estimate the parameter $\dot{m}_{\rm HL}$ as
$\dot{m}_{\rm HL} \gsim 0.1$.
Furthermore, if the canonical luminosity is established in
1E~1740.7$-$2942,
then the intrinsic luminosity is $\Gamma \gsim 0.1$
(or $L \gsim 1.25 \times 10^{38} {\rm ~erg~s}^{-1}$
for $M=10M_{\odot}$).
The observational luminosity, on the other hand,
is about $3 \times 10^{37} {\rm ~erg~s}^{-1}$
(or normalized luminosity is 0.02).
Since the observational luminosity is the projected one and
equal to $2\Gamma \cos i$,
the inclination angle of the disk is
$i \gsim 80^{\circ}$,
that is consistent with the geometrical configuration.
Similary, the canonical mass accretion rate is estimated as
$\dot{M}/\dot{M}_{\rm HL} \lsim 0.8$
(or $\dot{M}/\dot{M}_{\rm E}=\Gamma \gsim 0.1$,
$\dot{M} \sim 10^{19}{\rm ~g~s}^{-1}$).
Since $M_{\rm jet} = 10^{16}{\rm ~g~s}^{-1}$ (appendix),
a small fraction of accretion mass is ejected by jets.
天文学研究室へもどる
