ホイル=リットルトン降着 (Hoyle-Lyttleton accretion)は,
HoyleとLyttletonが1939年に提案したもので,
重力天体への質量降着の基本的なメカニズムである.
十分調べ尽くされたように思える,このきわめて古典的な問題が,
“中心天体の輻射場”という光を当てることにより,
新たな現代的問題として甦った.
Reference:
Nio, Matsuda, Fukue 1998
Fukue and Ioroi 1998 (English)
降着円盤をもつ重力天体へのホイル=リットルトン降着を調べたところ, 光源が球対称でない場合には,降着の様相が劇的に変化することがわかった. 降着円盤の軸方向からガスが流入するpole-on降着の場合は, 質量降着率は球対称な場合より小さくなる. 一方,降着円盤の縁方向からガスが流入するedge-on降着の場合は, 質量降着率は球対称な場合より大きくなる. 降着円盤の非等方な輻射場によって, 質量降着は円盤面内で起こりやすくなるので, 円盤面が自動的に維持される. このことは,宇宙ジェットの方向性の維持にとっても都合がよい. 実際,銀河中心のX線源1E 1740.7-2942などでは, 降着円盤へのホイル=リットルトン降着が起こっていると予想される.
■ホイル=リットルトン降着とは?
重力天体への質量降着は, 現代宇宙物理学のもっとも重要な現象の一つである. というのも,質量降着は,物質の重力エネルギーの解放して, 膨大なエネルギーを放出するからだ. もし中心の天体が(ブラックホールなどの)コンパクト星なら, 降着ガスのもつ静止質量エネルギーの何割かが解放される. さらにそのような質量降着システムからは, しばしば高エネルギーの質量流出−ジェット−が生じている.

さて,もし星間空間に単独の天体があれば,
その天体の重力はまわりのガス粒子を引き寄せるだろう.
もしガスに対して天体が動いていれば,
上流から飛んできたガス粒子は,
双曲線軌道を描いて天体の下流で交わるだろう.
そして天体の下流で交わったガス粒子は,衝突し合体するだろう.
このときの対称軸を降着軸(accretion axis)と呼ぶ.
さらに,合体粒子の降着軸上の位置が天体から十分遠方で,
運動エネルギーが十分大きければ,そのまま通り過ぎるだろう.
逆に天体に十分近くて,位置エネルギーが大きければ,
ガス粒子は天体の重力場に捕らわれ,
降着軸に沿って天体に落下(降着)することになる.
これが,ホイル=リットルトン降着の古典的描像である.
(Hoyle, Lyttleton 1939; Bondi, Hoyle 1944).
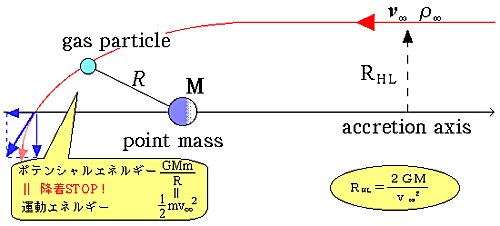
もう少し定量的に調べてみよう. 上の図のように, 密度がρ∞で速度がv∞で流れてくるガス流の中に, 質量がMで光度がLの天体が浸されているとしよう. このとき,古典的なホイル=リットルトン降着半径 (Hoyle--Lyttleton accretion radius) RHLは,
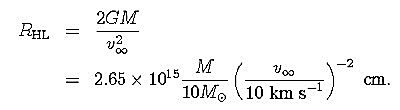
遠方から流れてくるガスのうち, ホイル=リットルトン降着半径を半径とする円内に流入するガスは, 中心の天体に落ち込むことになるから, 中心天体への質量降着率 (mass accretion rate) は,
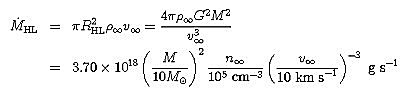
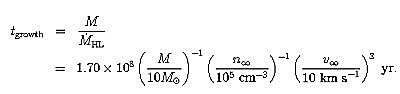
■中心天体が光っているとき:輻射圧の影響
古典的なホイル=リットルトン降着では, 中心の天体は重力作用のみを及ぼすだけで光っていないのだが, もし中心の天体が光っていれば,ガス粒子は,重力作用に加え, 光の圧力−光圧,放射圧,輻射圧(radiation pressure)− をも受けることになる. 実際,(古典的な)ホイル=リットルトン降着によって, 中心の天体にガスが落下すれば, (最初は中心の天体は光っていなくても) 重力エネルギーの解放によって降着ガスが高温になり, その結果,中心の天体が光り輝くことは大いにあり得る.
中心の天体が光っているとき, 輻射圧は外向きに働くので, ガス粒子は一般に降着しにくくなる. そのため,中心天体の輻射圧を考慮すると, たとえば降着半径は古典的なものより小さくなるし, その結果,質量降着率も小さくなる. (e.g., Taam et al. 1991).
具体的に,中心天体の(実際の)光度をL, エディントン光度をLEとする. (エディントン光度は,中心天体の重力と輻射圧が釣り合う光度で, LE=4πcGMmp/σT で表される; mpは陽子の質量, σTはトムソン散乱の断面積) 中心天体の光度をエディントン光度で規格化した, 無次元化した光度Γ:
を導入する. この無次元化した光度Γを使えば, 輻射圧を考慮したホイル=リットルトン降着半径 RHLradは,
のように修正される. ちなみに,質量降着率は,降着半径の2乗に比例するので, 古典的な質量降着率より, (1−Γ)2 だけ小さくなる.
■輻射抵抗の効果
最近,仁尾友美ら(Nio et al. 1998, PASJ 50, 495)が, 中心天体が光っている場合のホイル=リットルトン降着において, 輻射圧の効果に加え輻射抵抗(コンプトン抵抗)の影響を調べた.
中心天体の光度がエディントン光度に近く, ガスの速度が光速に比べて無視できないときは, 輻射抵抗の影響が効いてくる. また,ダストのように,有効的な比断面積が大きいとき, つまり輻射場の影響を受けやすい場合も,輻射抵抗の影響が現れる. 実際,輻射抵抗の影響が最初に指摘されたのも, 太陽系内のダストの振る舞いに対してである (いわゆるポインティング=ロバートソン効果).
仁尾らの研究によると, 降着半径は,輻射圧の効果で減少する一方で, 輻射抵抗の効果で増加することがわかった. また流入速度v∞が大きいほど, 輻射抵抗の影響も大きくなる. 流入速度が光速の1割ぐらいまでの範囲では, 輻射抵抗の効果を取り入れた降着半径は,近似的に,
のように表される.
■降着円盤へのホイル=リットルトン降着
以上述べたようなホイル=リットルトン降着に関する従来の研究では, 中心の天体は,星のように,球対称に光っていることが, 暗黙のうちに仮定されていた. ところが,よく知られているように, 重力天体に向けて質量降着が起こるときは, 中心の天体のまわりには,しばしば降着円盤が形成される. 降着ガスの重力エネルギーの解放によって降着円盤は光り輝くのだが, 降着円盤から放射される光は,非等方的(anisotropic)であり, 強い方向依存性をもっているのだ.
具体的には,降着円盤の全光度をL, 円盤の対称軸から測った極角をθとすると, 中心から距離Rの点での輻射流束Fは,
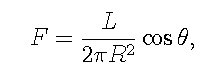
降着円盤をもつ重力天体へのホイル=リットルトン降着のように, 光源が球対称でない場合には, 降着の様相が劇的に変化することが予想される.
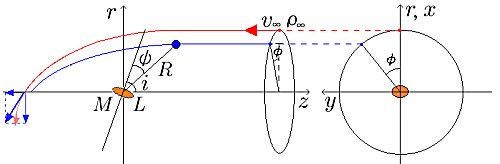
問題を定量的に調べるために, 上の図のような状況を考えてみる. すなわち,質量Mの天体のまわりに光度Lの降着円盤が形成されており, そのシステムは,密度がρ∞で速度がv∞ のガス流に浸されているとする. ガスは完全電離していて,また放射に対しては透明だとする. 降着円盤は,ガス流の方向すなわち降着軸に対して, 一般的には傾いており, 降着軸と降着円盤の対称軸のなす角度を傾斜角iとする. 上の図のように降着軸をz軸とする円筒座標(r,φ,z)を用いるが, 直角座標(x,y,z)や球座標(R,θ,φ)も援用する (R2=r2+z2).
■輻射場分布
最初にガス粒子の位置における(降着円盤の)輻射場を求めておこう.
まず,降着円盤の対称軸方向の単位ベクトルiと, ガス粒子の方向の単位ベクトルsは, 直角座標でそれぞれ,
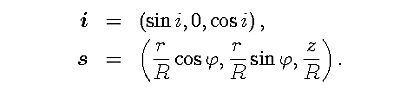
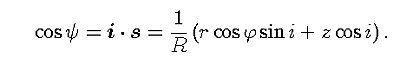
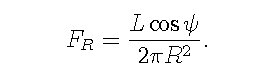
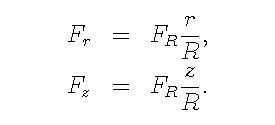
なお,これらの話は,降着半径が降着円盤より十分大きいときの話で, 降着円盤の近傍では, 降着円盤の輻射場は非常に複雑になり (cf. Tajima, Fukue 1998), もっと詳しい扱いが必要になる.
■運動方程式
輻射場中における粒子の運動方程式は, 粒子の速度をv, 粒子の質量をm, 重力ポテンシャルをφ, 輻射エネルギー密度をE, 輻射流束ベクトルをF, 輻射ストレステンソルをPとして, 速度に関してv/cの1次のオーダーまでの近似で,
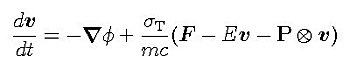
仁尾ら(1998)では,輻射抵抗の項を残したのだが, ここでは簡単のために落とし, 輻射場の非等方性に注目して輻射圧の影響だけ考えよう. そうすると,運動方程式は,円筒座標系で,
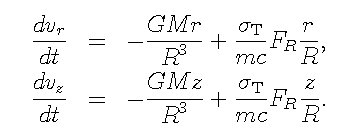
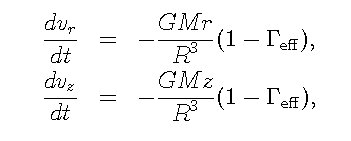
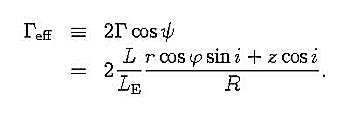
十分上流(zが大)でのさまざまな初期値(r,φ)に対して, 上の運動方程式を数値的に解き, ガス粒子の軌道を求める. そして粒子の軌道が下流で降着軸に交差する場所で, 粒子のz速度がそこでの脱出速度より大きいか小さいかを比べ, ガス粒子が中心天体に落下するか否かを判定するのである.
パラメータは, 規格化した光度Γ, 無限遠での速度v∞(表には出てこない), 降着円盤の傾斜角iである. このうち,傾斜角については, i=0の場合(円盤面がガス流の面している;pole-on)と i=90°の場合(円盤面が真横を向いている;edge-on)の, 両極端の場合のみを考えた.
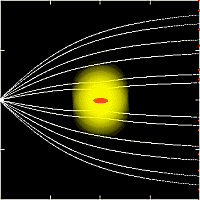
■計算結果

上の図は,ホイル=リットルトン降着半径RHLで規格化した
降着半径Raccを,
規格化した光度Γの関数として求めたものである.
点線は,従来の球対称な場合で,先に述べたように,
(1−Γ)に比例して降着半径は小さくなる.
破線はpole-on降着(i=0)の場合で,
降着円盤の輻射場は円盤に鉛直方向に強くなっている
(正面から見たら降着円盤は明るく見える).
その結果,流入するガスに対して円盤面が正面を向くpole-on降着では,
ガスの受ける輻射圧はより強くなるので,
図のように,球対称な場合より,降着半径はさらに小さくなるのである.
多数の実線は,edge-on降着(i=90°)の場合で,
実線の違いは降着軸のまわりの円周角φに対応する.
このedge-on降着では,降着半径がφに強く依存するので複雑だが,
大ざっぱには,縁方向から見れば降着円盤は暗く見える.
その結果,輻射圧の効果は弱まり,球対称な場合より,
降着半径は大き目になる.
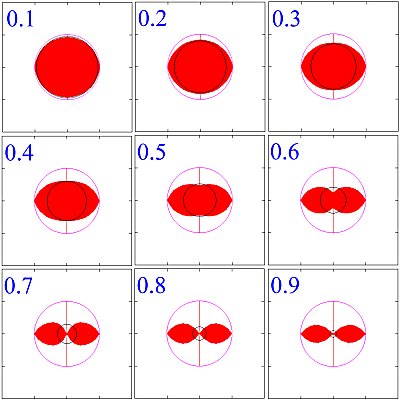
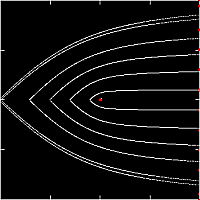
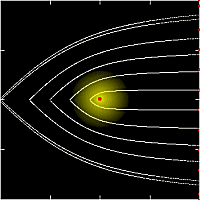
上の図は,
降着円盤の真横から流入するedge-on降着(i=90°)について,
降着領域の断面(赤い部分)を示したものである
(パネルの左上の数字はΓの値).
外側の円は古典的なホイル=リットルトン降着半径RHLで,
内側の円は球対称な場合の降着半径を表す.
円盤面内(φ=90°;図の左右)で入射する粒子は,
降着円盤からの輻射を受けないので,
降着半径は古典的な半径RHLに一致する.
一方,円盤の上方(φ<90°;図の上下方向)で入射する粒子は,
降着円盤の輻射場の影響を受けて,
降着半径は小さくなる.
その結果,降着領域の断面積は,図のように上下につぶれたものになる.
より細かく言えば,降着領域の断面積は,
Γが小さいと上下に潰れた楕円形になり,
Γが0.5ぐらいで上下に凹んだ形状になり,
Γが0.65ぐらいからは真上方向では降着できなくなるため,
双葉のような形状になる.
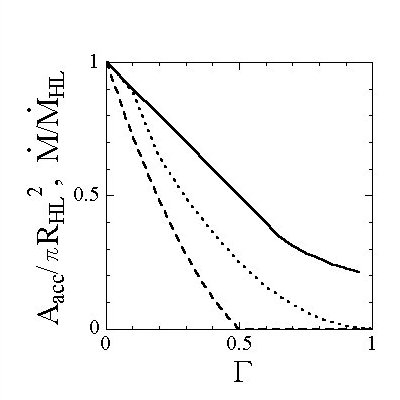
上の図は,降着断面積を規格化した光度Γの関数として表したものである. すなわち,縦軸は, 古典的なホイル=リットルトン降着の断面積で規格化した降着断面積で, 降着断面積に質量流束をかけたものが質量降着率になることから, ホイル=リットルトン降着の質量降着率で規格化した質量降着率でもある. 点線は従来の球対称な場合で,先に述べたように, (1−Γ)2に比例して小さくなる. 破線はpole-on降着(i=0)の場合で, 球対称の場合より小さい. さらに実線はedge-on降着(i=90°)の場合で, 球対称の場合より大きい. このedge-on降着の場合で特筆すべきことは, 規格化した光度Γが1のとき (降着円盤の光度がエディントン光度に等しいとき)でも, 質量降着が可能な点である. 最後に,上の計算結果を近似的に表すと, 以下の近似式で表すことができた.
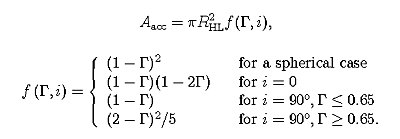
降着円盤へのホイル=リットルトン降着では, 以上のようにして, 降着円盤の光度L(Γ)の関数として質量降着率が得られる. 一方,与えられた質量降着率によって,降着円盤の光度は定まる. それらを併せると,降着円盤の光度が無矛盾に決まることになる. そのようにして得られるカノニカル光度に関する議論は, ここでは省略する.
その他, 円盤面(と宇宙ジェット)の方向性の維持に関する議論や, 銀河中心のX線源1E 1740.7-2942への応用など, 詳細な議論も省略する(英語版参照).
 天文学研究室へもどる
天文学研究室へもどる